Since the Wine data set seemed to be very easy to categorize, it was the first data set presented to this back propagation program. The second set to be presented is the proteins data set. It is very complex and a nettalk like approach was needed. The third data set described is the Vowels data set. Because the Vowel data set seemed to be a slightly more complex data set than wine and was larger (more data to train on), it was trained many times with different parameter settings, so that each of the parameters influence could be monitored. All three data sets and the more complex Vowels data set are presented here with graphs and results. But first, some of the problems encountered will be described.
Through this project some problems were encountered, a selected few are
presented here. The reason for this is that it gives some insight of what was
achieved, and maybe to prevent them from arising next time.
[ toc | previous |
next | up ]
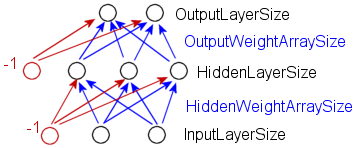
The problem of implementing this feature, it not big, its just irritating. It involves a lot of small changes everywhere in the code and it is very important to place the +1 count in the right places, otherwise a segment fault or overwriting memory could be the result. A good way to handle this is probably to program the code with this in the mind and use separate constants for the size of the layers and weight arrays as shown in the picture below.

This would mean that for the example above that has 2 inputs and 2 outputs,
the InputLayerSize is 2, the HiddenLayerSize is 3 and the OutputLayerSize is 2.
The HiddenWeightArraySize (this is the weight array size for each neuron in the
hidden layer) should be set to one more than the size of the input layer, namely
3. The OutputWeightArraySize should be set to the HiddenLayerSize plus one. Then
all these constants should be used instead of the +1 counts that is used in the
current program. This would increase the structure, understanding and
scalability of the code.
[ toc |
previous | next |
up ]
This is very similar to the problem in the Kohonen chapters. How should the
data be presented to the user? Since the gnuplot program was quite familiar at
this point, the actual presenting of the data was not the issue. The real issue
was probably the way the data was generated. In the beginning a redirect to a
file was used quite commonly. Each programmer had their own format of the files
and even if the files still exist there is very little comment on each file and
the reason why it was computed was probably not remembered more than a couple of
hours after it was generated. This has made a lot of information useless.
Instead maybe it is a good idea to beforehand decide what structure and what
data is to be stored and then store it in different directories. With each
directory there should be an information file, that describes when it was made
and the changes since last time or the purpose of this generation. This,
together with a small program that could automatically generate graphs from this
directory would have made our time more well spent.
[ toc |
previous | next |
up ]
Another completely different question is, between what
values is considered right output? How much may the outputs deviate from the
desired output and still be called right? In the resulting program, if the
highest output is above zero and is the same as the desired then it is
considered to be correct.
[ toc |
previous | next |
up ]
This was the main of our problems, and also the main cause for the late presentation of this report. The program was written by three different people, in three different ways. There was no initial discussion how the program was to be structured. The main reason for this was that parts of the group already was busy with another project. This mistake is probably very common in new projects, but should be avoided at all costs. The lack of collaboration in the beginning usually changes the outcome of the project in a not desired way.
In physical terms this problem revealed itself in countless number of hours
debugging, because no one had the full knowledge of the code. Later though, when
everyone had turned the code upside down for the tenth time. The general
knowledge of the code was probably far greater and also quite good in the
learning perspective, though it could also probably been accomplished by a
thoroughly overhaul in the beginning of the project.
[ toc |
previous | next |
up ]
After implementing the back propagation algorithm to a neural network processing the wine data we could see some interesting behaviours. The most interesting thing to look at when evaluating a neural network is the possibility to classify the input correct, both for the training set and the test set. In the beginning of the training phase is the correctness fluctuating pretty much, but after (in this case) approximate 120 iterations it stabilizes.
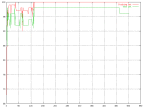 |
| The percent of correctness over time for the wine data set. |
Another interesting thing to look at in a neural network is the RMS (root mean square) error for the nodes. The RMS error is a measurement for how correct the nodes are calculated compared to the correct output. The graph below shows that it takes a while before the error stops fluctuate and stabilizes. After it stops fluctuating it decreases very slowly.
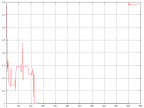 |
| The change of the RMS error over time. |
It seems to have converged at 250 iterations or so, but is displaying very good results even at 100 iterations. This could probably be better if the learning rate and momentum were chosen differently.
The average of the networks with 5 hidden units and up is
for the test set, around 100%. This is with a random selection of the test set.
The best percentage reached with the training set is 100.0% and it was performed
by almost all networks from iteration 10 and up.
[ toc | previous |
next | up ]
The secondary structures '_', 'e' and 'h' are in the graphs below labelled as their respective outputs, 0, 1 and 2.
When a data set is first presented it is really hard to know how complex it is in number of neurons in the hidden layer. Especially if no previous experience is present. So this is the task of the following graphs, to show how many neurons that actually were needed for this data set.
As can be seen the ten neuron graph is somewhat flat, it has converged this early. It was expected to be too small but the effect was not known. The 20 hidden neuron graph is a lot better than the first, but there is still some 'slowness' about it if compared to the last two. The 30 and 50 neuron graphs seem to perform quite well. The 50 neuron graph seems to perform faster, but the computational time made most of the following graphs based on a hidden layer of 30 neurons.
One really interesting thing about this is, that below 100 iterations the first network (the one with 10 hidden units) actually performs better than the other. Although in the long run it will probably not have a chance since the other outputs are still improving at the end of 100 iterations. One could also speculate about the generalization prediction of the first network. Would it really perform worse than the others if more data was fed into it? Hard to answer but the graphs above does suggest the possibility. The number of neurons has in spite of this been chosen to 30 for most of the other graphs.
In order to actually see the effect of the randomness in the network, four batches on the same data set with the same parameters were run. This is the result.
 |
 |
| Percent correct predictions of the protein training set with 30 hidden units, generated four times. | Percent correct predictions of the protein test set with 30 hidden units, generated four times. |
As can be seen, they are not that different. This was a good and interesting thing to see though. Batch number one (the red) seems to deviate the most, but still shows the same charachteristics as the other. This means that the other graphs that show differences between different parameters could be taken quite literary since there was no real differences.
 |
 |
| RMS Error of the protein training set with 30 hidden units, generated four times. | RMS Error of the protein test set with 30 hidden units, generated four times. |
This is the RMS Error for the four runs, and they clearly show traits of similarity with the percentage graphs above. Yet again the red is the one most distingishable one and it performs slightly worse than the other here as well.
The Kohonen results presented in chapter 3 hinted that the secondary structure 'h' should be easy to recognize. The results below that show the percent of correct predictions in each of the secondary structures, has the ability to verify that.
 |
| Percentage of correct predictions for each separate output of the protein set with 75 hidden units |
This graph is with definite certainty the graph that shows the most in this report. Here we can se that the secondary structure 'h' (number 3 in the graph) is very easy to distinguish from the others and almost directly turn towards the 100% mark. The second proof that this set is easy it the test set curve. It starts dropping very early indicating that it is over trained. Maybe it is possible to make a run where the third output is not trained at every iteration, to make the match more evenly. Though that is beyond the resulting program at this point.
Also the first and second output (secondary structure '_' and 'e') seems to follow each other, this could suggests that the errors in one of them is predicted as the other. Then when the time progresses it learns how to distinguish them more accurately. As for the test sets for both of the outputs they seem not to display any hints of overtraining. The small dip in the beginning is probably just the result of the distribution changes that is going on. The rapid changes in one output might 'steal' predictions from the other outputs and result as dips in them.
The Percentage correct and the RMS Error from the graph presented above is quite interesting to note.
 |
 |
| Percent correct from a long iteration run of the protein set with 75 neurons in the hidden layer | RMS Error from a long iteration run of the protein set with 75 neurons in the hidden layer |
The training error is is getting smaller all the time but the test error seem to stagnate after 800 to 1000 iterations. The test set percent correct is actually rising all the time and the question is when to stop training this network. Since the third output is quite over trained at 400 iterations when the other seem to present good results, it is tough to decide, but the prudent course of action is probably to stop around 350 iterations.
The average of the networks with 30 hidden units and up is
for the test set, around 47%. The best percentage reached with the training set
is 93.7% and it was performed by the 75 hidden neuron network at iteration 1200.
[ toc |
previous | next |
up ]
The behaviours of the back propagation networks were interesting to study, because it showed expected and unexpected things,
the variation of neurons needed in a well working network, the coupling between
learning rate or momentum and the number of neurons in the hidden layer.
When implementing the back propagation algorithm to analyze the vowel data set we wanted to see how changes in the network structure affected the
behaviour of the network and the output result. To see the differences dependent
on the variables (momentum, learning rate, number of neurons and parameters A and B) we plotted them out.
Only one variable was changed at a time.
[ toc | previous |
next | up ]
This test was done from as few as 5 neurons up to 75 neurons in different intervals (5, 8, 10, 15, 20, 30, 50, and 75). Out of this graph we could see that the 20 neuron network gave us the best results.
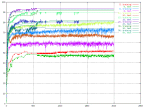 |
| The percent of correctness over time for different number of neurons in the hidden layer. |
As can be seen by this, over the 15 neuron limit there was no
noticeable increase or decrease in performance. It also shows that the fewer neurons
that was tried the bigger was the fluctuation. It would suggest that a choice of
15 neurons is quite adequate for this data set. The change in other parameters
could also influence some, so it is to early to say.
[ toc | previous |
next | up ]
For learning rate we tried a wide range of values, from 0.001 to 0.5. One thing that was speculated about was the influence of the learning rate with different sized data sets since the choice to train after each element of the data set was made.
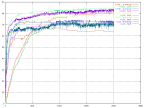 |
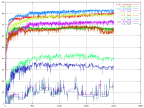 |
| The percent of correctness over time for different values for the learning rates. | The percent of correctness over time for different values for the learning rates. |
It was seen by these graphs that the fluctuation was connected to the size of the learning rate, the larger learning rate, the larger fluctuation. The fluctuation is also larger for the test set than for the the training set. The really big learning rates are not useful at all because of the low correctness and the huge fluctuation. On the other hand, if the learning rate is very small (under 0.005) it takes to long time to train the network.
There was no real way to prove the learning rate behaviour
on different sized data sets with just this information, but it is discussed in
chapter 6.
[ toc | previous |
next | up ]
Momentum is an important thing in the neural network because it minimizes the chances to get stuck in a local minimum. Therefore the interest in how the momentum affects the behaviour of the output was big. We tried to find what would happen if it was way to large.
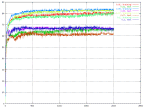 |
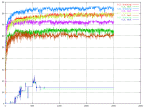 |
| The percent of correctness over time for different values of the momentum. | The percent of correctness over time for different values of the momentum. |
When it was set to 0.9, really strange behaviour was
observed. It was also observed that the fluctuation was related to the size of the momentum. The bigger momentum, the bigger fluctuation, except then the momentum was
way to large. The best result was when the momentum was between 0.5 and 0.05.
[ toc | previous |
next | up ]
Some of the less interesting changeable variables are the A and B parameters in the activation function. These are the parameters that are presented in chapter 4.
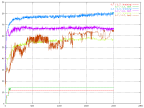 |
| The percent of correctness over time for different values of the A and B constant. |
When changing these some of the output was not even
possible to use in any application. Either because the correctness of the output
was very low or because it fluctuated too much. What is done is change the
effect that the previous output has on the neuron and also the current output.
For extreme values this would result in a very sensitive or a completely
unsensitive network.
[ toc | previous |
next | up ]
From the previous results a mix of the best values was used to generate the following graphs. This is a way to get the best result possible without having adaptive momentum and/or learning rate. In the same time it gave us a possibility to see the behaviour dependent on the change in the different variables.
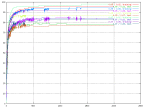 |
| The percent of correctness over time for the optimized network using different values of the learning rate and momentum. |
From this graph the following could be seen. The
difference seems to change quite a lot when the different values are tried, but
the performance is quite satisfactory.
[ toc | previous |
next | up ]
One other interesting thing, except the correctness of the output, is the RMS (root mean square) error. This shows how big the error between the output and the desired output is. This error is calculated here only on the training portion of the data set. In other words, the RMS error is almost always decreasing, even after the network is over trained.
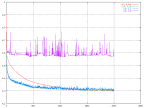 |
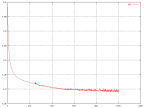 |
| The change in RMS over time for different values of the learning rate. | The change in RMS over time for the original network. |
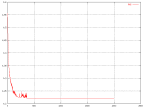 |
| The change in RMS over time for the optimized network. |
Most of the graphs have a point where there is a much larger amount of fluctuations than in the rest of the graph. This point appears usually just before the slope starts to flatten out.
The average of the networks with 15 hidden units and up is
for the test set, around 48%. This is with the designated test set. The graphs
above are made with a random selection of the test set. The best percentage
reached with the training set is 97.0% and it was performed by the 20 hidden
neuron network at iteration 300.
[ toc | previous |
next | up ]