Many of the conclusions are embedded in chapter 3 and 5 which present the results of the Kohonen and the Back Propagation networks. Some chosen data is also presented here.
The kohonen's SOFM is a quite simple and understandable method of a self organizing network. But it can really be complicated to implement and it really requires a lot of computational power to be able to compute anything.
This was actually a quite nice thing to do, it gave an extra advantage to tackle the problem. Especially the distribution of the input dimensions were good to have seen, so that errors could have been spotted right away. Also the search for question marks and missing commas in the data set made the data seem more familiar and made the handling of it somewhat easier.
The size of the network is quite important. The size we chose was 13, and it was chosen because it seemed to be a nice compromise between the program execution time and the resolution of the graphs. Since the time to calculate a larger network increases in exponential manner, this was thought to be a good decision.
There is a lot of calculations that need to be done in the Kohonen's SOFM. It is the calculation of who is the winning neuron that takes the most time. And as described in chapter 3, the use of the absolute value instead of the RMS calculation speeded up the program by more than seven times.
There is a lot that can be done with a Back Propagation Network. But there are also a few things to keep in mind when programming them.
When choosing the number of neurons in the hidden layer it is better to have too many, if you have the computer power to run it, than to have to few. The number of neurons in the hidden layer is connected to the number in the output and input layer. It is also connected to the complexity of the input data. A good example of this is to compare the network for the wine (not so complex) with the network for the vowels (more complex).
When comparing the two networks (wine and vowels) we realized that a good value of the learning rate is connected to the size of the network and the complexity of it. We can not say how big/little it should be under witch circumstances you have to test your way through it (or trust well trained feeling).
Since the network is trained on each data element rather than on the complete data set, it is important to keep the learning rate small. Otherwise the data could fluctuate a lot and the results are jumping up and down because different elements tell it to go to a different direction. Based on the experience from this project a good rule of thumb for choosing the initial learning rate is 10/number of data elements in the data set. This will provide a quite accurate number that can be used for training.
Because the momentum is used to overcome local minimums in the training of the network, it takes a very important part in the training. To have a big momentum makes it easier to overcome minimums and sometimes possible to overcome big local minimums. But, it makes the output fluctuate a lot and makes it harder to get a good result of the correctness. In the other hand using a small momentum makes it harder, if possible, to overcome local minimums. So what would be preferred is a momentum that is adaptive and in that way takes the best part from both worlds.
An adaptive momentum gains size when travelling downwards and is losing size when travelling upwards. This makes it more likely to overcome minimums.
Optimization is something that almost every network has to go through to give good final result. One way of minimizing the effort is to let the learning rate, momentum and even the number of neurons be adaptive. This makes the network slower so it is an adjustment of time to do manual preparations and time to let the network train. The choice is connected to the size and complexity of the input data, the size of the network e.g. so the choice is very hard to predict but a way in the middle is to prefer.
Over training a network is something that is not wanted, because it deteriorates the final results of a neural network. We tried to over train a network, just to see how it reacted. It was actually pretty hard to get some dramatically changes. We succeeded to get some of the networks over trained after many attempts. This shows that it is not always easy to over train a network, but it is very important that this does not happen.
 |
 |
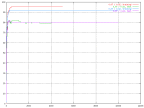
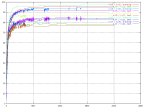
| A graph showing a network (the green) with a dip that can indicate an over trained network. | A graph showing some networks with early dips. |
One really good example of overtraining is described in chapter 5, where the third output shows significant proof of being over trained.
There must be about 2 or 3 whole days of computer processing time in these graphs presented in the report and at least an additional week processing time for testing. If this was 18 months ago it would be the double. It would be nice to know what results the next year students will produce, if they have access to better computers, or if it will be the same results.
One thing can really be said. The Kohonen's SOFM really take time to execute. The protein data set took 13 hours to compute and several other sets had to be cut down in order to being able to compute some output at all. To get this all running as fast as possible, there was a lot of optimizations done. Formulas were looked over to see if something could be calculated together and to use variables instead of functions in the really time critical part of the program.